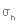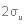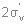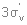|
|
 |
|
|||||||||||||
 |
 |
||||||||||||||
 |
 |
||||||||||||||
|
|||||||||||||||
| · |
Задача по предмету "Строение молекул"
Основываясь на уравнении Хартри-Фока и методе Хюккеля, предскажите свойства двух заданных молекул, а также вид их ИК-, КР- и ЯМР-спектров. При решении задачи необходимо использовать теорию групп и таблицу характеров. Решение: МОЛЕКУЛА С8Н8 Уравнение Хартри-Фока служит для нахождения вида молекулярных орбиталей: 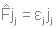 «Фокиан» для данной молекулы будет выглядеть так: 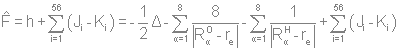 Действие кулоновского и обменного оператора на одноэлектронную функцию (орбиталь) определено следующим образом: 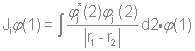 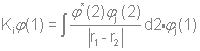 Молекулярное уравнение – полный гамильтониан системы: 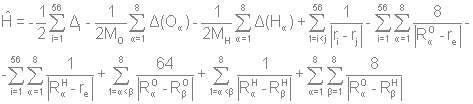 Метод Хюккеля Пронумеруем атомы углерода следующим образом: 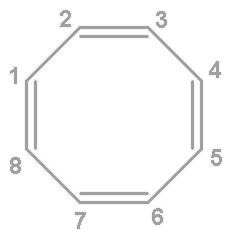 Матрица Хюккеля будет выглядеть следующим образом:  где 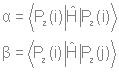 i, j – относятся к соседним атомам. Построим симметризованный базис. Точечная группа симметрии – D8h. Расклассифицируем базисные функции по ее циклической подгруппе C8. Для этого сначала построим таблицу характеров, воспользовавшись уже существующей таблицей для C4:
Тогда несложно понять, что таблица характеров для группы C8 выглядит следующим образом:
Используя стандартную процедуру построения симметризованного базиса и таблицу характеров, получаем новый вид симметризованных базисных орбиталей. 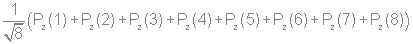 X2(Г2): 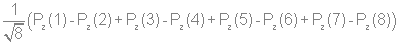 X3(Г3): 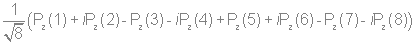 X4(Г4): 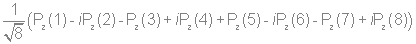 X5(Г5): 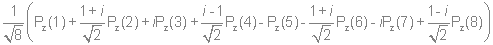 X6(Г6): 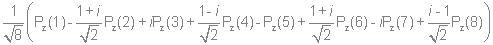 X7(Г7): 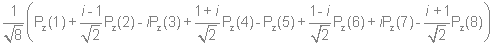 X8(Г8): 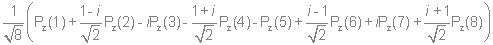 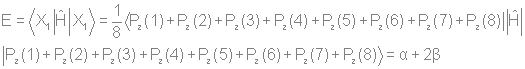 По аналогии (не забывая, что слева в скобках Пуассона стоит комплексосопряженная функция, получаем: 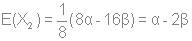 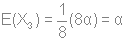 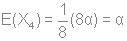 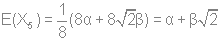 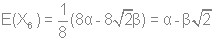 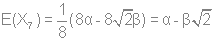 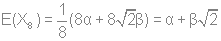 Для вырожденных состояний можно переопределить новые базисные функции следующим образом, чтобы избавиться от мнимой части: 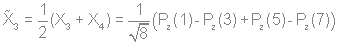 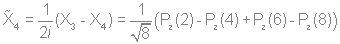 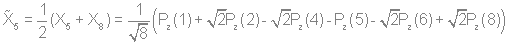 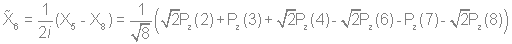 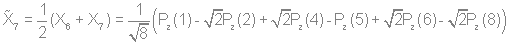 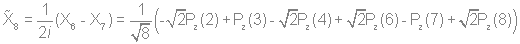 Итак, мы имеем 8 уровней энергии, расположенные следующим образом: 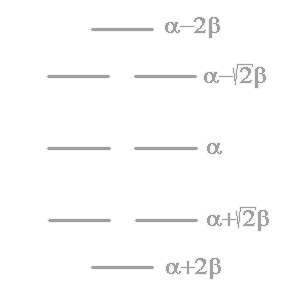
Колебательная задача Построим колебательное представление для данной молекулы. Подгруппа D4h. Оси C2 проходят через атомы:
Разложение по неприводимым представлениям даст следующее: 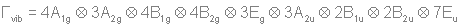 Из таблицы характеров определяем число ИК-колебаний: ИК - 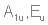 (14 колебаний) (14 колебаний)КР - 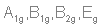 (18 колебаний) (18 колебаний)ЯМР спектр будет иметь один пик МОЛЕКУЛА Si3O3 Геометрия данной молекулы не указана, а в природе такой не существует. Примем равновесную геометрию за следующую: 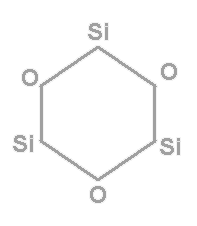 Уравнение Хартри-Фока: 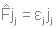 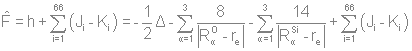 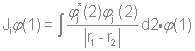 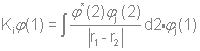 Молекулярное уравнение: 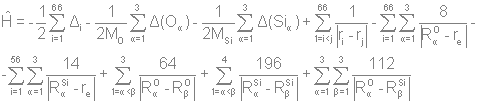 Метод Хюккеля Метод Хюккеля применим для сопряженных пи-систем, к которым данная молекула не относится. Колебательное представление Точечная группа симметрии D3h. Построим колебательное представление:
Раскладывая по таблице характеров, получаем, что: 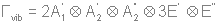 Из таблицы характеров следует, что в ИК-спектре будут видны 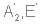 (7 колебаний),
а в КР - (7 колебаний),
а в КР - 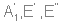 (10 колебаний). (10 колебаний).В ЯМР спектре можно получить только информацию по кремнию – соответственно один пик от трех эквивалентных групп. контекстная реклама |
· |
 |
|



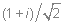
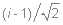
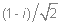
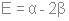
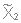 (8 узлов)
(8 узлов)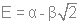
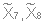 (6 узлов)
(6 узлов)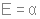
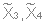 (4 узла)
(4 узла)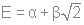
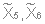 (2 узла)
(2 узла)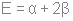
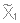 (0 узлов)
(0 узлов)